通信题_Good Integer

前几天太鸽了，没怎么老老实实搞竞赛QwQ……Deadline将近，我只好来分享一道题。我的数学水平尚且非常有限，可能不能理解其本质，还请谅解……有大佬可以教教我……

这个题有意思的地方在于场上只过了一个队，而补题十天后也只有一个队补了这个题（？）尽管这个题好像通常构造方法都行不通，但是这个题实则不难……可能主要问题在于题解写的不够好，或者选手没有补题兴趣？

这道题是这样的：

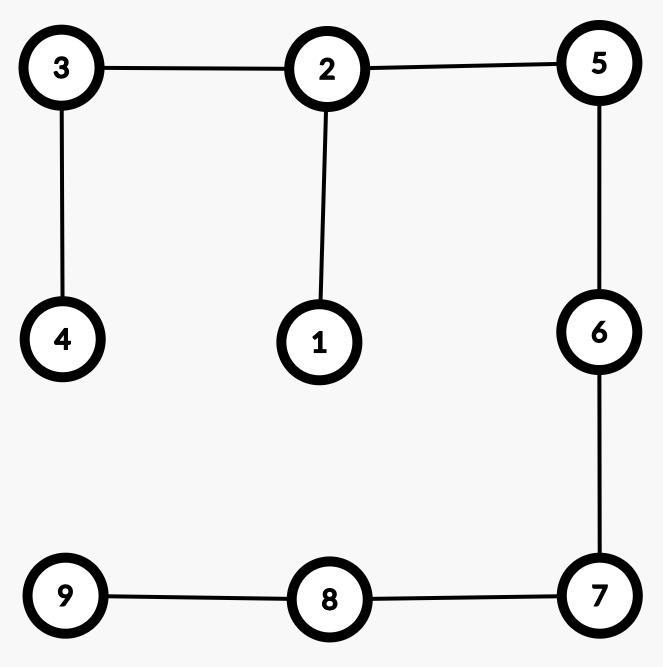
一个如图所示的图，现在要求将一个长度为 的01序列转换为一个长度不超过 的图上路径，然后再要求实现这个变换的逆变换。

建议自己想一想，还是挺有意思的。

---

大概所有选手都会一开始去算一算从每个点出发的长度为n的路径共有多少个……设这个图为G，G的邻接矩阵为A（未列出为0）

那么长度为n+1的序列个数就是中所有数字的和。为了充分了解增长的趋势，可以使用WolframAlpha作为工具求出所有特征值，发现最大的特征值为2，对应的特征向量为，这样一来就知道路径数目的增长趋势也是 ，同所要求的长度没有渐进性的差距。

所以应当如何做呢？我们从特征向量上进行考虑。对于，由于这是特征值2对应的特征向量，使用矩阵进行一次乘积之后得到的就是原向量*2。考虑矩阵乘法的过程，就和这个伪代码转移是一样的：

C  = [3, 6, 4, 2, 5, 4, 3, 2, 1]
C' = [0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in V:
    for j in G[i]:
        C'[j]+=C[i]

这就启发我们可以建立如下的一个新的图G2：

G2中的每一个点为一个数对(i,j)，其中i为G中的一个点，j为[0,Vec[i)中的一个整数。

同时我们可以连边，对于每一个G中的点对(u,v)，如果这两个点之间是有边的，我们就可以把G2中每一个(u,x)连向某一个(v,y)，同时确保每一个G2中的点入度不超过2。由于特征向量的性质，G2中每一个点的入度将会恰好为2！

实现如下：

void build_graph(){
    for(int i=1;i<=9;i++){
        for(auto ct:G[i]){
            for(int j=0;j<vec[i];j++){
                for(int k=0;k<vec[ct];k++)
                if(fr[ct][k].size()<2){
                    G2[i][j].PB(MP(MP(ct,k),fr[ct][k].size()));
                    fr[ct][k].PB(MP(i,j));
                    break;
                }
            }
        }
    }
}

这时就自然的想到，一个点的入度为2，那么我们将G2中所有边反向，得到一个反图G2’。每个点的出边恰好两条，编号为0和1后，我们从G2’的(1,0)点出发，每次按照01序列对应的边走，不就唯一的得到一个长度为n+1简单路径了？

这种方法的问题在于，有时候0边和1边指向的点在G中的编号是相同的。比如(1,0)的两个出边就可能是(2,0)和(2,1)，因为1在G的度数是1。

为了解决这个问题，我们可以发现在G2中，对于所有G中相邻的点(u,v)，每个点(u,x)有且只有一条边连向某一个以v为第一维坐标的节点(v,?)。因此如果我们知道上一个过程中走到的最后一个节点的第二维度的坐标，就可以唯一地以相反的顺序推出所编码01序列了。为了将这个信息（第二维度的坐标）编码，我们需要在路径的开始，节点1之前加上一个相应长度的路径如(1-2-5-6-7-8)。

这样，由于所有第二维度的坐标不超过6，最终答案的长度一定是在n+10之内的。

下附代码。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define set0(x) memset(x,0,sizeof(x))
#define F first
#define S second
#define PB push_back
#define MP make_pair
#define rep(i, a, b) for(int i = a; i < (b); ++i)
#define trav(a, x) for(auto& a : x)
#define all(x) x.begin(), x.end()
#define sz(x) (int)(x).size()
vector<int> G[10];
vector< pair<pii,int> > G2[10][10];
vector< pii > fr[10][10];

int vec[11] = {0,3,6,4,2,5,4,3,2,1,0};
void ins(int a,int b){
    G[a].push_back(b);
    G[b].push_back(a);
}

void build_graph(){
    for(int i=1;i<=9;i++){
        for(auto ct:G[i]){
            for(int j=0;j<vec[i];j++){
                for(int k=0;k<vec[ct];k++)
                if(fr[ct][k].size()<2){
                    G2[i][j].PB(MP(MP(ct,k),fr[ct][k].size()));
                    fr[ct][k].PB(MP(i,j));
                    break;
                }
            }
        }
    }
}

void solve1(){
    int n;string s;
    cin>>n>>s;
    pii pos(1,0);
    string ans;
    for(int i=0;i<s.size();i++){
        ans+=(char)('0'+pos.F);
        pos = fr[pos.F][pos.S][s[i]-'A'];
    }
    ans+=(char)('0'+pos.F);
    reverse(all(ans));
    ans+=((string)"25678").substr(0,pos.S);
    cout<<ans<<endl;
}

void solve2(){
    int n;string s;
    cin>>n>>s;
    pii pos(s[0]-'0',(map<char,int>{{'1',0},{'2',1},{'5',2},{'6',3},{'7',4},{'8',5}}[s[s.size()-1]]));
    while(s[s.size()-1]!='1')s = s.substr(0,s.size()-1);
    string ans;
    for(int i=1;i<s.size();i++){
        for(auto ct:G2[pos.F][pos.S]){
            if(ct.F.F == s[i]-'0'){
                ans+=ct.S+'A';
                pos = ct.F;
                break;
            }
        }
    }
    reverse(all(ans));
    cout<<ans<<endl;
}
string s;
int main() {
    ins(1,2);ins(2,3);ins(2,5);ins(3,4);
    ins(5,6);ins(6,7);ins(7,8);ins(8,9);
    cin>>s;
    build_graph();
    if(s == "first"){
        solve1();
    }else{
        solve2();
    }
    return 0;
}