一句话题意:给你一棵n个点的树,和树上的m条路径。问有多少对路径的交长度大于k?
n m 150000, 4s
我实现的做法是题解做法,代码比较长。但是我还是比网上的另一个同学短了100行。。
大概合并的线段树还是可以使用pbds里面的平衡树来代替,但是我写代码之前并不知道……
写完之后去读了最短的代码(代码长度0.5倍),发现是中国选手。没读懂,问出题人,出题人也读不懂。。
找到他的QQ就问了一下他,然后发现了一个很妙的做法,然后发现好多选手都是写的这个做法,只有我太憨了去实现题解。。。下面描述一下那个做法。
首先进行一步转化。
一个树上的路径,[|路径|>=k] = #长度为k的子段-#长度为k+1的子段
因此只需要对树上的所有长度为k或者k+1的路径求一下被覆盖了多少次,就得到答案。比如被覆盖了c次,那么贡献的绝对值就是c(c-1)/2,符号取决于长度是k(正)还是k+1(负)。
首先进行重链剖分,然后对于一条路径,长度为k的段大概是这样的:
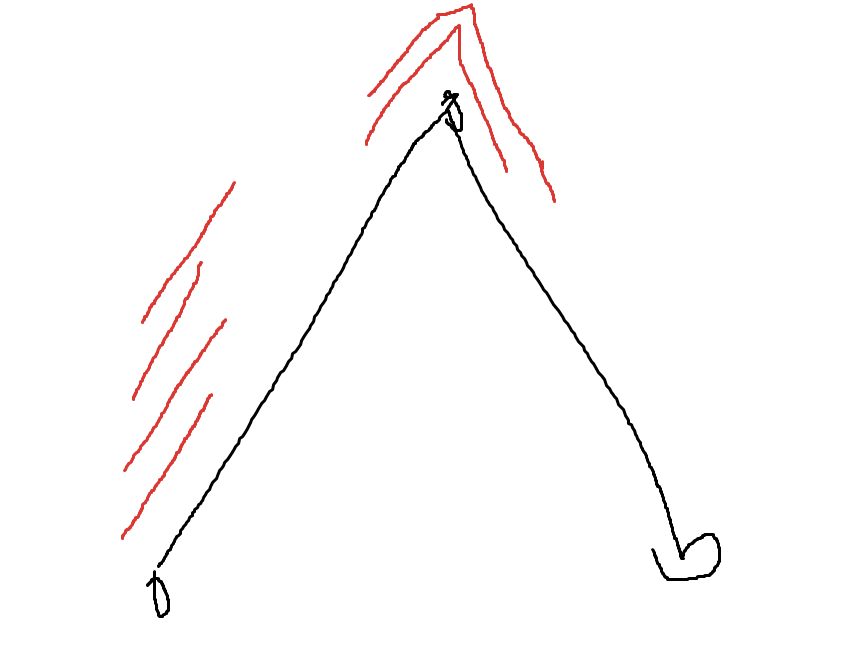
竖直的覆盖的段上的贡献可以直接使用剖分上的差分来做。现在问题就出在拐弯的段上。
拐弯的段的处理很巧妙,考虑我们把整个区间拆分成重链上。
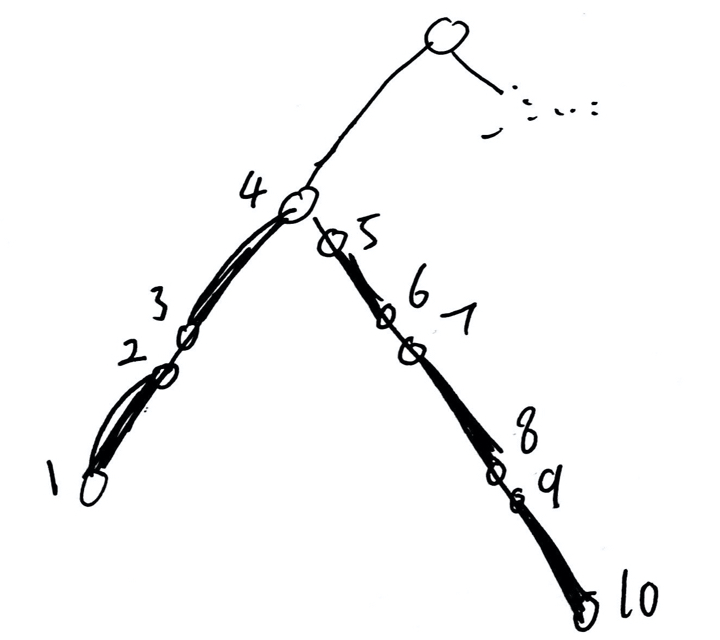
然后考虑任何一个长度为k的跨越lca(4号点)的子段,我们采用他开始节点所在重链、终止节点所在重链、开始节点的深度来差分记录,开一个数组套map套map就行了,复杂度也是两个log……太妙了。
下面是我的题解做法代码
#pragma comment(linker, "/stack:200000000")
#pragma GCC optimize("Ofast,no-stack-protector")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native")
#pragma GCC optimize("unroll-loops")
#include <bits/stdc++.h>
using namespace std;
#define set0(x) memset(x,0,sizeof(x))
#define F first
#define S second
#define PB push_back
#define MP make_pair
#define rep(i, a, b) for(int i = a; i < (b); ++i)
#define trav(a, x) for(auto& a : x)
#define all(x) x.begin(), x.end()
#define sz(x) (int)(x).size()
typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef vector<int> VI;
template<typename T> void read(T &x){
x = 0;char ch = getchar();ll f = 1;
while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args) {
read(first);
read(args...);
}
const int N = 150050;
int n,m,k,s[N],t[N],lc[N],u,v;
vector<int> G[N],G2[N],T[N],oT[N];
int fa[N][19],d[N],dfn[N],sz[N],tim = 0;
void dfs0(int num,int cf = 0){
dfn[num] = ++tim;
fa[num][0] = cf;
sz[num] = 1;
for(int j=0;fa[num][j];j++)fa[num][j+1] = fa[fa[num][j]][j];
for(auto ct:G[num]){
if(ct==cf)continue;
d[ct] = d[num]+1;
dfs0(ct,num);
sz[num]+=sz[ct];
}
}
inline int lca(int u,int v){
if(d[u]<d[v])swap(u,v);
for(int i=18;i>=0;i--)if(fa[u][i] && d[fa[u][i]]>=d[v])u = fa[u][i];
for(int i=18;i>=0;i--)if(fa[u][i]!=fa[v][i])u = fa[u][i],v = fa[v][i];
return u == v?u:fa[u][0];
}
inline int anc(int u,int x){
for(int i=18;i>=0;i--) if(fa[u][i] && d[fa[u][i]]>=x)u = fa[u][i];
return u;
}
struct Fenwick{
int s[N];
vector<pii> log;
inline void update(int pos, int dif) {
log.emplace_back(pos,dif);
while(pos<N){
s[pos]+=dif;
pos+=pos&(-pos);
}
}
void reset(){
int pos,dif;
for(auto ct:log){
pos = ct.F;
dif = -ct.S;
while(pos<N){
s[pos]+=dif;
pos+=pos&(-pos);
}
}
log.clear();
}
inline int query(int pos) {
int res = 0;
while(pos){
res+=s[pos];
pos-=pos&(-pos);
}
return res;
}
}A;
vector<pii> F[N],F2[N];
struct node{
int ls = 0,rs = 0;
int val = 0;
}nds[10000010];
int cnt = 0,rts[N];
#define mid ((cl+cr)/2)
int query(int id,int l,int r,int cl = 0,int cr = n){
if(id == 0 || (l<=cl && cr<=r))return nds[id].val;
return ((l<=mid)?query(nds[id].ls,l,r,cl,mid):0)+((r>mid)?query(nds[id].rs,l,r,mid+1,cr):0);
}
void add(int &id,int x,int cl = 0,int cr = n){
if(!id)id = ++cnt;nds[id].val++;if(cl == cr)return;
if(x<=mid)
add(nds[id].ls,x,cl,mid);
else
add(nds[id].rs,x,mid+1,cr);
}
int merge(int a,int b){
if(!a || !b)return a|b;
nds[a].val+=nds[b].val;
nds[a].ls = merge(nds[a].ls,nds[b].ls);
nds[a].rs = merge(nds[a].rs,nds[b].rs);
return a;
}
void reset(){
memset(nds,0,sizeof(nds[0])*(cnt+1));
cnt = 0;
}
ll ans = 0;
int crt = 0;
void dfs1(int num){
int tgt;
auto add_it = [&](int ct){
if(d[num]+d[ct]-2*d[crt]>=k){
if(d[num]>=d[crt]+k){
tgt = anc(num,d[num]-k+1);
ans+=nds[rts[num]].val;
ans-=query(rts[num],dfn[tgt],dfn[tgt]+sz[tgt]-1);
}else{
tgt = anc(ct,d[crt]+k-(d[num]-d[crt]));
ans +=query(rts[num],dfn[tgt],dfn[tgt]+sz[tgt]-1);
}
}
};
int mx = -1,ms = -1;
for(auto ech:G2[num]){
dfs1(ech);
if((int)T[ech].size()>mx){
mx = T[ech].size();
ms = ech;
}
}
if(ms!=-1)rts[num] = merge(rts[num],rts[ms]);
for(auto ct:T[num]){
add_it(ct);
add(rts[num],dfn[ct]);
}
if(ms!=-1){
//cout<<ms<<endl;
swap(T[num],T[ms]);
for(auto ct:T[ms])T[num].PB(ct);
}
for(auto ech:G2[num]){
if(ech == ms){
//cout<<"JMP"<<endl;
continue;
}
for(auto ct:T[ech]){
add_it(ct);
T[num].PB(ct);
}
rts[num] = merge(rts[num],rts[ech]);
}
}
int main() {
read(n,m,k);
for(int i=1;i<n;i++){
read(u,v);
G[u].PB(v);
G[v].PB(u);
}
d[1] = 1;
dfs0(1);
for(int i=0;i<m;i++){
read(s[i],t[i]);
if(dfn[s[i]]>dfn[t[i]])swap(s[i],t[i]);
lc[i] = lca(s[i],t[i]);
F[d[lc[i]]].emplace_back(s[i],t[i]);
F2[lc[i]].emplace_back(s[i],t[i]);
}
for(int i=n;i>=1;i--){
for(auto ct:F[i]){
int l = ct.F,r = ct.S;
ans+=A.query(dfn[l]);
ans+=A.query(dfn[r]);
}
for(auto ct:F[i]){
int l = ct.F,r = ct.S;
if(d[l]>=i+k){
l = anc(l,i+k);
A.update(dfn[l],1);
A.update(dfn[l]+sz[l],-1);
}
if(d[r]>=i+k){
r = anc(r,i+k);
A.update(dfn[r],1);
A.update(dfn[r]+sz[r],-1);
}
}
}
A.reset();
auto cmp = [&](int a,int b)->bool{return dfn[a]<dfn[b];};
for(int i=1;i<=n;i++){
crt = i;
vector<int> cu,scope;
scope.PB(i);
for(auto ct:F2[i]){
cu.PB(ct.F);
T[ct.F].PB(ct.S);
oT[ct.F].PB(ct.S);
}
sort(all(cu),cmp);
cu.erase(unique(all(cu)),cu.end());
vector<int> stk;
stk.PB(i);
rts[i] = ++cnt;
auto pb = [&](int a){
rts[a] = ++cnt;
scope.PB(a);
stk.PB(a);
};
for(auto ct:cu){
int dd = lca(ct,stk.back());
while(d[stk.back()]>d[dd]){
if(d[stk[stk.size()-2]]>d[dd]) G2[stk[stk.size()-2]].PB(stk.back());
else G2[dd].PB(stk.back());
stk.pop_back();
}
if(d[stk.back()]<d[dd]) pb(dd);
if(d[stk.back()]<d[ct]) pb(ct);
}
while(stk.size()>=2){
G2[stk[stk.size()-2]].PB(stk.back());
stk.pop_back();
}
dfs1(i);
for(auto ct:cu){
ans+=1ll*A.query(dfn[ct])*oT[ct].size();
for(auto ed:oT[ct]){
if(d[ed]>=d[i]+k){
int cc = anc(ed,d[i]+k);
A.update(dfn[cc],1);
A.update(dfn[cc]+sz[cc],-1);
}
}
}
A.reset();
reset();
for(auto ct:scope){
G2[ct].clear();
rts[ct] = 0;
T[ct].clear();
oT[ct].clear();
}
}
cout<<ans<<endl;
return 0;
}
下面是高水平选手的nb做法代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define N 300000
int n,m,k,a[N][2],fa[N],sz[N],top[N],d[N],prf[N],f1[N],q1[N],q2[N];
vector<int> g[N],b[N];
map<int,map<int,int> > f2[N];
LL ans;
void dfs1(int u){
d[u]=d[fa[u]]+1;
sz[u]=1;
for (int v:g[u])
if (v!=fa[u]){
fa[v]=u;
dfs1(v);
sz[u]+=sz[v];
}
}
void dfs2(int u){
if (!top[u]) top[u]=u;
b[top[u]].push_back(u);
int t=0;
for (int v:g[u])
if (v!=fa[u]&&sz[v]>sz[t]) t=v;
if (!t) return;
prf[u]=t; top[t]=top[u]; dfs2(t);
for (int v:g[u])
if (v!=fa[u]&&v!=t) dfs2(v);
}
int lca(int x,int y){
for (;top[x]!=top[y];x=fa[top[x]])
if (d[top[x]]<d[top[y]]) swap(x,y);
return d[x]<d[y]?x:y;
}
int go(int x,int k){
int len=d[x]-d[top[x]];
if (len<k) return go(fa[top[x]],k-len-1);
return b[top[x]][len-k];
}
int add1(int x,int y){
int len=d[x]-d[y];
if (len<k) return x;
int z=go(x,len-k+1);
++f1[x]; --f1[z];
return z;
}
void add2(int u1,int u2,int v1,int v2){
if (top[u1]>top[v1]){
swap(u1,v1); swap(u2,v2);
}
if (d[u1]>d[u2]) swap(u1,u2);
++f2[top[u1]][top[v1]][d[u1]];
--f2[top[u1]][top[v1]][d[u2]+1];
}
void add(int x,int y){
int z=lca(x,y);
x=add1(x,z); y=add1(y,z);
int u=x,v=y;
int n1=0,n2=0;
for (;top[u]!=top[z];u=fa[top[u]]) q1[++n1]=u;
for (;top[v]!=top[z];v=fa[top[v]]) q2[++n2]=v;
if (u!=z) q1[++n1]=u; if (v!=z) q2[++n2]=v;
for (int i1=1,i2=n2;i1<=n1;++i1){
int u1=q1[i1],u2=top[u1];
if (d[u2]<=d[z]) u2=prf[z];
for (;i2;--i2){
int v1=q2[i2],v2=top[v1];
if (d[v2]<=d[z]) v2=prf[z];
if (d[u1]+d[v1]-d[z]*2<k) continue;
int len=d[u1]+d[v1]-d[z]*2;
int w1=go(v1,len-k),w2=0;
len=d[u2]+d[v1]-d[z]*2;
if (len>=k){
w2=go(v1,len-k);
add2(u1,u2,w1,w2);
break;
}
len=d[u1]+d[v1]-d[z]*2;
w2=go(u1,len-k);
add2(u1,w2,w1,v1);
u1=fa[w2];
}
}
}
LL C(LL x){return x*(x-1)/2;}
void dfs3(int u,int t){
for (int v:g[u])
if (v!=fa[u]){
dfs3(v,t);
f1[u]+=f1[v];
}
ans+=C(f1[u])*t;
}
void calc(int t){
for (int i=1;i<=n;++i){
for (auto j:f2[i]){
LL sum=0,lst=0;
for (auto k:j.second){
ans+=(k.first-lst)*C(sum)*t;
lst=k.first;
sum+=k.second;
}
}
f2[i].clear();
}
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for (int i=1;i<n;++i){
int x,y; scanf("%d%d",&x,&y);
g[x].push_back(y); g[y].push_back(x);
}
dfs1(1); dfs2(1);
for (int i=1;i<=m;++i){
scanf("%d%d",a[i]+0,a[i]+1);
add(a[i][0],a[i][1]);
}
dfs3(1,1); calc(1);
memset(f1,0,sizeof f1);
++k;
for (int i=1;i<=m;++i)
add(a[i][0],a[i][1]);
dfs3(1,-1); calc(-1);
printf("%lld\n",ans);
return 0;
}
发表回复